
下載app免費領取會員


在計算機圖形學中,Dynamo是一種常見的旋轉實現(xiàn)方法。它通過應用數(shù)學變換來實現(xiàn)對象的旋轉,使得對象在三維空間中以任意軸進行旋轉。
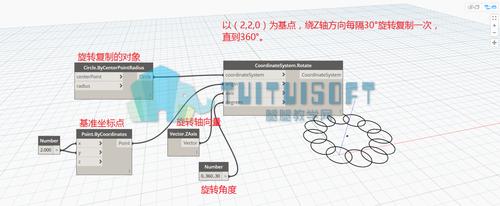
旋轉是圖形學中的一項基本操作,它能夠改變對象的位置和方向。在Dynamo方法中,旋轉是通過應用一個旋轉變換矩陣來實現(xiàn)的。這個矩陣定義了一個用于旋轉的軸,以及旋轉的角度。
為了實現(xiàn)Dynamo的旋轉方法,首先需要確定旋轉軸的位置和方向。旋轉軸可以是任意的向量,它可以通過定義兩個點來確定。旋轉軸的方向是與這兩個點的向量方向相同的單位向量。
一旦旋轉軸被確定,接下來就可以計算旋轉變換矩陣了。旋轉變換矩陣是一個三維變換矩陣,它可以將對象旋轉指定的角度。在計算旋轉變換矩陣時,需要使用旋轉角度和旋轉軸。
計算旋轉變換矩陣的方法比較簡單。首先需要將旋轉角度轉換為弧度制,然后使用三角函數(shù)計算旋轉矩陣的各個元素。旋轉變換矩陣的計算公式如下:

其中θ是旋轉角度,ux,uy,uz是旋轉軸的坐標。
一旦旋轉變換矩陣被計算出來,就可以將其應用到對象上。應用旋轉變換矩陣時,需要將對象的每個頂點坐標與矩陣相乘。相乘的結果就是旋轉后的對象坐標。
除了旋轉變換矩陣,還可以使用四元數(shù)來實現(xiàn)Dynamo的旋轉方法。四元數(shù)是一種用于表示旋轉的數(shù)學工具,它可以更高效地進行旋轉計算。使用四元數(shù)進行旋轉時,可以將旋轉角度和旋轉軸轉換為四元數(shù)表示,然后將四元數(shù)與對象進行插值運算。
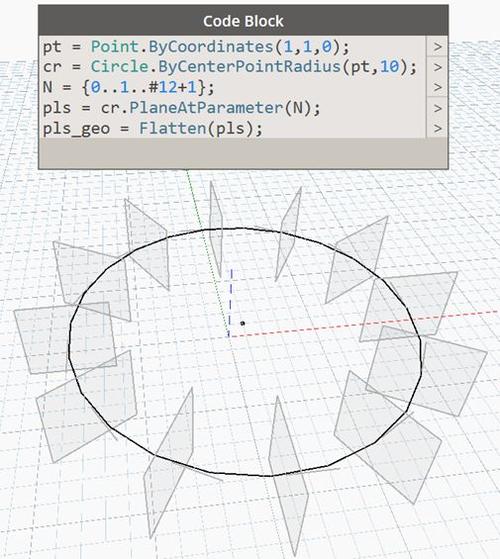
總結起來,Dynamo的旋轉實現(xiàn)方法使用旋轉變換矩陣或四元數(shù)來實現(xiàn)對象的旋轉。旋轉變換矩陣通過計算旋轉軸和旋轉角度來確定,然后將其應用到對象上。而四元數(shù)則更高效地進行旋轉計算,通過插值運算來實現(xiàn)對象的平滑旋轉。
本文版權歸腿腿教學網(wǎng)及原創(chuàng)作者所有,未經(jīng)授權,謝絕轉載。

上一篇:Dynamo教程 | dynaform5.9.4安裝指南






推薦專題













































